|
O Método de Dwight |
|
Tomemos um condutor tubular de raio externo,
re e raio interno ri,
suficientemente afastado do condutor de retorno.
Fazendo re- r i = t, a
espessura da parte maciça do tubo, e
para ri  r r
 re, adotando x = r -
ri. a corrente que atravessa uma
casca da seção reta de espessura x vale
re, adotando x = r -
ri. a corrente que atravessa uma
casca da seção reta de espessura x vale
|
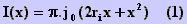 |
sendo j0 a densidade uniforme de corrente que
atravessa o condutor. O fluxo interno à casca vale:
o fluxo externo à casca, dentro do condutor vale:
cujo resultado após a integração é:
Chamaremos S0(t) os termos dentro do primeiro
colchete e S0(x) os termos dentro de segundo
colchete na expressão (4), podemos ver que o segundo termo é
dependente da variável de integração x enquanto o
primeiro, não. Para obtermos a queda de potencial reativa numa casca
dx basta multiplicar a expressão (4) por 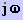 .
.
Suponhamos que uma densidade de corrente 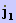 atravesse a seção reta
do condutor, tal que
atravesse a seção reta
do condutor, tal que 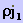 seja a queda de potencial devido à passagem de uma densidade da
corrente no meio de resistência específica
seja a queda de potencial devido à passagem de uma densidade da
corrente no meio de resistência específica 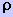 e que essa queda de potencial tenha o sinal oposto ao
termo S0(x).
e que essa queda de potencial tenha o sinal oposto ao
termo S0(x). 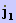 vai gerar um fluxo externo à casca que deve ser calculado de (3),
substituindo o termo entre colchetes por S0(x) .
Após a integração dois novos termos serão gerados
S1(t) e S1(x) com apenas
S1(x) dependendo explicitamente da variável de
integração, x.
vai gerar um fluxo externo à casca que deve ser calculado de (3),
substituindo o termo entre colchetes por S0(x) .
Após a integração dois novos termos serão gerados
S1(t) e S1(x) com apenas
S1(x) dependendo explicitamente da variável de
integração, x.
Para obtermos mais termos basta repetir o processo
de integração para os termos do tipo Sn(x)
gerados.
Repetindo-se o processo e somando os termos obtemos
finalmente o valor de IZ' que vale:
com 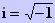 e
e 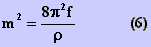
sendo 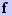 a
frequência adotada e
a
frequência adotada e 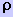 a
resistência específica do condutor.
a
resistência específica do condutor.
A série de coeficientes em k na expressão
(5) foi truncada no primeiro termo. Para uma visualização da série
completa consulte-se a referência básica desse trabalho:
Dwight, 1918. A expressão (3) permite calcular a queda de potencial
IR, considerando-se os limites de integração 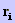 e
e 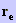 . O valor de R'/
R é obtido da razão
. O valor de R'/
R é obtido da razão 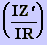 após a racionalização do denominador e eliminação do termo
imaginário.
após a racionalização do denominador e eliminação do termo
imaginário.
O método descrito acima pode ser utilizado para
condutores sólidos e para fitas. No caso de fitas obtem-se:
onde, 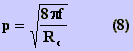 e
e 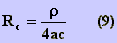
onde 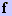 é a
frequência adotada e Rc é a resistência
por unidade de comprimento da fita de dimensões c
(espessura) x a (largura). As expressões
(7) (8) e (9) permitem calcular a razão R'/
R no caso de fitas.
é a
frequência adotada e Rc é a resistência
por unidade de comprimento da fita de dimensões c
(espessura) x a (largura). As expressões
(7) (8) e (9) permitem calcular a razão R'/
R no caso de fitas.
Fechar
Janela
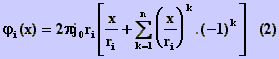
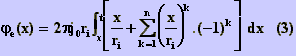
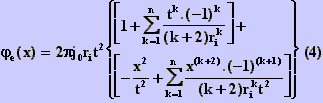
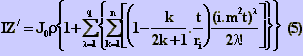
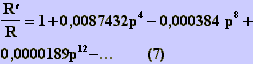
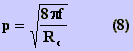 e
e